인수분해의 목적은 보통 어떤 원소를 더 기초적이고 간단한 조각으로 분해하는 데 있다. 예를 들어, 수를 소수들의 곱으로, 다항식을 인수분해 되지 않는 다항식으로 분해하는 것이다. 그리고 다항식의 경우는, 변수
 에 대하여
에 대하여  가 근삿값 일 때, 근삿값을 참값에 가깝게 계산하기 위함과 방정식 등 을 풀기 위해 사용한다. 정수 집합에서는 산술의 기본 정리, 다항식의 집합에서는 대수학의 기본 정리와 관련이 있다. 그러나 모든 환에서 인수분해가 더 이상 분해되지 않는 원소들의 곱으로 유일하게 표현되는 것은 아니다. 유일한 인수분해가 성립하는 가환환을 유일 인수 분해 정역이라고 한다.
가 근삿값 일 때, 근삿값을 참값에 가깝게 계산하기 위함과 방정식 등 을 풀기 위해 사용한다. 정수 집합에서는 산술의 기본 정리, 다항식의 집합에서는 대수학의 기본 정리와 관련이 있다. 그러나 모든 환에서 인수분해가 더 이상 분해되지 않는 원소들의 곱으로 유일하게 표현되는 것은 아니다. 유일한 인수분해가 성립하는 가환환을 유일 인수 분해 정역이라고 한다.다항식의 인수 분해[편집]
다항식의 계수(coefficient)의 집합을 어느 범위로 한정하느냐에 따라 소인수분해의 결과가 달라질 수 있다. 예를 들어, 계수를 유리수로 한정할 경우  과
과  는 모두 인수분해 되지 않으므로 기약다항식(Irreducible polynomial)이 된다. 그러나 실수로 확장하면
는 모두 인수분해 되지 않으므로 기약다항식(Irreducible polynomial)이 된다. 그러나 실수로 확장하면  는
는  로 인수분해 되고,
로 인수분해 되고,  는 여전히 기약다항식이 된다. 계수를 복소수로 더 확장하면 비로소
는 여전히 기약다항식이 된다. 계수를 복소수로 더 확장하면 비로소  는
는  로 인수분해 된다. 계수에 복소수를 허용하면 대수학의 기본 정리(fundamental theorem of algebra)에 의해 모든 복소계수 다항식이 일차식으로 항상 인수분해 가능하다.
로 인수분해 된다. 계수에 복소수를 허용하면 대수학의 기본 정리(fundamental theorem of algebra)에 의해 모든 복소계수 다항식이 일차식으로 항상 인수분해 가능하다.
 과
과  는 모두 인수분해 되지 않으므로 기약다항식(Irreducible polynomial)이 된다. 그러나 실수로 확장하면
는 모두 인수분해 되지 않으므로 기약다항식(Irreducible polynomial)이 된다. 그러나 실수로 확장하면  는
는  로 인수분해 되고,
로 인수분해 되고,  는 여전히 기약다항식이 된다. 계수를 복소수로 더 확장하면 비로소
는 여전히 기약다항식이 된다. 계수를 복소수로 더 확장하면 비로소  는
는  로 인수분해 된다. 계수에 복소수를 허용하면 대수학의 기본 정리(fundamental theorem of algebra)에 의해 모든 복소계수 다항식이 일차식으로 항상 인수분해 가능하다.
로 인수분해 된다. 계수에 복소수를 허용하면 대수학의 기본 정리(fundamental theorem of algebra)에 의해 모든 복소계수 다항식이 일차식으로 항상 인수분해 가능하다.이차식[편집]
이차식 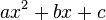 가 주어져 있을 때, 이 이차식의 값을 영으로 만드는 두 원소
가 주어져 있을 때, 이 이차식의 값을 영으로 만드는 두 원소 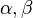 가 있다면 다음과 같이 인수분해 된다.
가 있다면 다음과 같이 인수분해 된다.
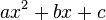 가 주어져 있을 때, 이 이차식의 값을 영으로 만드는 두 원소
가 주어져 있을 때, 이 이차식의 값을 영으로 만드는 두 원소 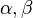 가 있다면 다음과 같이 인수분해 된다.
가 있다면 다음과 같이 인수분해 된다.
또한 이차방정식의 근의 공식을 이용하여 다음과 같이 계수로 표현가능하다.
고차식[편집]
삼차, 사차식의 경우에는 근의 공식을 이용할 수도 있다. 그러나 계산과정이 길고 손으로 직접하기에는 어려움이 따른다.
특별한 고차식에 적용할 수 있는 다양한 테크닉들이 있는데, 이러한 몇몇 공식들은 중고교 교과과정에서 자주 등장한다. 예를 들어,
와 같은 공식들이 있다. 이와 같은 공식들이 적용되지 않는다면 적당히 추측하는 방법을 동원하여 조립제법을 쓰는 경우도 있다.
위 공식을 사용하여 1보다 큰 모든 정수 n에 대해  이 다음과 같이 항상 소수가 아님을 알 수 있다.(헝가리 Kürschák 경시대회 1978년 문제)[1]
이 다음과 같이 항상 소수가 아님을 알 수 있다.(헝가리 Kürschák 경시대회 1978년 문제)[1]
 이 다음과 같이 항상 소수가 아님을 알 수 있다.(헝가리 Kürschák 경시대회 1978년 문제)[1]
이 다음과 같이 항상 소수가 아님을 알 수 있다.(헝가리 Kürschák 경시대회 1978년 문제)[1]- (증명) n이 짝수일 경우
 은 짝수이다. n이 홀수일 경우,
은 짝수이다. n이 홀수일 경우,  이므로 역시 합성수가 된다.
이므로 역시 합성수가 된다.
잘 알려진 인수 분해 공식[편집]
모든 공식에 복부호 동순이 적용된다. 2차식
3차식
4차식














![a^3+b^3+c^3-3abc = (a+b+c)(a^2+b^2+c^2-ab-bc-ca)=1/2(a+b+c)[(a-b)^2+(b-c)^2+(c-a)^2]](https://upload.wikimedia.org/math/7/a/d/7ad625efa9254f22afe66bc58dc18fe7.png)
댓글 없음:
댓글 쓰기