참조 : http://kin.naver.com/qna/detail.nhn?d1id=13&dirId=130103&docId=216836441&qb=7Jyg66as7IiY&enc=utf8§ion=kin&rank=1&search_sort=0&spq=0
간단하게
따라서 0, 음의정수 양의정수, 분수는 모두 유리수고
유한소수와 무한소수 중 순환하는 소수도 모두 유리수입니다.
0.3333...을 간혹가다 무리수라고 하시는 분이 있는데  으로 표현 가능하기 때문에 0.3333...도 유리수 입니다.
으로 표현 가능하기 때문에 0.3333...도 유리수 입니다.
통분
분모가 다른 분수의 크기를 비교하거나 덧셈, 뺄셈을 할 때 통분을 이용한다. 둘 이상의 분수를 각각 크기가 같은 분수로 만들면 분모가 같은 경우를 찾을 수 있다.
〈 과
과 를 통분하기〉
를 통분하기〉
① 분모의 곱을 공통분모로 하여 통분하기
〈
① 분모의 곱을 공통분모로 하여 통분하기
② 분모의 최소공배수를 공통분모로 하여 통분하기
부분분수
분수로 된 식을 분모나 분자의 차수를 낮추어서 계산 과정에서 노가다하는 경우를 줄이기 위해서 많이 사용된다.
주로 복잡한 분수식을 간편히 나누어서 어려운 계산을 좀 더 쉽게 한다거나, 역라플라스변환, 적분하기 힘든 분수함수라든가, 무한급수의 일반항 등을 구할 때 부분분수로 변환해서 사용한다.
그럼 간단한 공식을 보자.
1/A - 1/B 이 식을 통분하시면요,
1/A - 1/B = ( B - A ) / A*B 가 되시는 것 아시죠~??
이것을 완벽히 외우시면 됩니다.
이 식에서 양변을 ( B - A ) 로 나누시면 끝입니다~
그렇게 되면,
1/( B - A ) * (1/A - 1/B) = 1/(A*B) 로 원하시는 식이 됩니다.ㅎㅎ
분모의 유리화
유리화(Rationalization)는 무리수가 있는 분수에서, 분모 부분을 유리수로 바꾸는 과정을 말한다. 다양한 기교와 테크닉이 있고 이러한 과정을 통해 분수의 통분이나 값의 파악을 쉽게 만든다.
단항식 근호의 유리화[편집]
중등 교과에 나오는 기법으로서, 분모에 단항식의 근호가 있을 경우 동일한 값을 분모와 분자에 모두 곱한다. 이러한 과정을 통하여도 분수 자체의 값에는 변화가 없다. 예를 들어 다음과 같은 분수가 있다고 하자.
이 경우 분모와 분자에 모두  를 곱한다. 그리하여,
를 곱한다. 그리하여,
 를 곱한다. 그리하여,
를 곱한다. 그리하여,
위와 같이 계산된다. 제곱근을 제곱했으므로 근호가 사라지고 다음과 같이 간단하게 값이 바뀐다.

다항식 근호의 유리화[편집]
두 개의 항이 있는 경우[편집]
인수분해 공식 를 이용하면 두 개의 제곱근을 포함한 분모를 유리화 할 수 있다. 즉, 분모와 분자에 그 켤레(conjugate)를 곱하여 분모를 유리수로 만들 수 있다. 예를 들어 다음과 같은 수가 있다고 하자.이 경우 분모와 분자에 모두
를 이용하면 두 개의 제곱근을 포함한 분모를 유리화 할 수 있다. 즉, 분모와 분자에 그 켤레(conjugate)를 곱하여 분모를 유리수로 만들 수 있다. 예를 들어 다음과 같은 수가 있다고 하자.이 경우 분모와 분자에 모두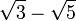 를 곱하여 해결한다. 그러므로
를 곱하여 해결한다. 그러므로세 개 이상의 항이 있는 경우[편집]
이 경우 두 개의 항을 하나의 항으로 보고 묶어서 계산할 수 있다. 다음의 예가 있다.이 경우 를 하나의 항으로 보고 계산한다. 즉,가 되므로 이 이후로는 이제 두 개의 항이 있는 경우와 동일하게 계산하면 된다.
를 하나의 항으로 보고 계산한다. 즉,가 되므로 이 이후로는 이제 두 개의 항이 있는 경우와 동일하게 계산하면 된다.삼중근을 포함하는 경우[편집]
분모에 삼중근을 포함하는 경우 등 과 같은 다양한 인수분해 공식을 활용하여 공격할 수 있다. 예를 들어, 다음과 같은 값이 주어져 있다고 하자.이 경우, 인수분해 공식을 활용하여 다음과 같이 계산한다.위와 같이 계산되게 된다.
등 과 같은 다양한 인수분해 공식을 활용하여 공격할 수 있다. 예를 들어, 다음과 같은 값이 주어져 있다고 하자.이 경우, 인수분해 공식을 활용하여 다음과 같이 계산한다.위와 같이 계산되게 된다.


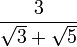




![\frac{1}{\sqrt[3]{2} - \sqrt[3]{3}}](https://upload.wikimedia.org/math/1/1/9/119c8a039e1c128d2862ba4269e50776.png)
![\frac{1}{\sqrt[3]{2} - \sqrt[3]{3}} = \frac{1}{\sqrt[3]{2} - \sqrt[3]{3}} \cdot \frac{\sqrt[3]{4} + \sqrt[3]{6} + \sqrt[3]{9}}{\sqrt[3]{4} + \sqrt[3]{6} + \sqrt[3]{9}} = \frac{\sqrt[3]{4} + \sqrt[3]{6} + \sqrt[3]{9}}{2 - 3}](https://upload.wikimedia.org/math/b/6/f/b6fee77a17d00ee21a7054757b5b85a2.png)
댓글 없음:
댓글 쓰기