
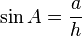


 에 대해,
에 대해,  축과 점과 원점을 잇는 직선간의 각을
축과 점과 원점을 잇는 직선간의 각을  라디안이라고 하면, 이때 사인, 코사인은 다음과 같이 정의된다
라디안이라고 하면, 이때 사인, 코사인은 다음과 같이 정의된다 .
.
또한, 나머지 함수들을 다음과 같이 정의한다.

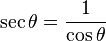
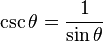

라디안(radian) 은 원둘레 위에서 반지름의 길이와 같은 길이를 갖는 호에 대응하는 중심각의 크기로 무차원의 단위이다. 호도(弧度)라고도 하며 ㎭로 줄여 쓰기도 한다. 보다 일반적으로 라디안 값은 원에서의 호와 반지름의 길이의 비율과 같다. 즉, θ = s /r 이다, 여기서 θ 는 라디안으로 주어진 각도, s 는호의 길이, r 은 반경이다.
라디안 각도를 표기할 때에는 숫자 뒤에 rad 혹은 c를 붙이거나, 아무것도 표시하지 않는 경우도 있다. 이 경우에는 도 단위와 혼동되지 않도록 도 단위에 °를 붙인다.



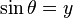

댓글 없음:
댓글 쓰기