일차함수 = 직선의 방정식
직교 좌표계
직교 좌표계(直交座標系, 영어: rectangular coordinate system), 혹은 좌표평면은 임의의 차원의 유클리드 공간 (혹은 좀 더 일반적으로 내적공간)을 나타내는 좌표계의 하나이다.
.

유클리드 공간

피타고라스의 정리
피타고라스의 정리(문화어: 세평방 정리)는 직각삼각형의 세 변의 관계를 나타내는 기본 정리이다. 이 정리는 평평한 입체도형 즉, 유클리드 공간 위에서 성립하며, 그 내용은 다음과 같다.


공식의 표현[편집]
c를 직각삼각형의 빗변의 길이, a와 b를 각각 나머지 두 변의 길이라 하면, 다음과 같이 공식으로 나타낼 수 있다.
또는, c에 대하여 풀이하면 다음과 같다.
단,위에서 c는 거리의 개념이므로 반드시 양수이어야한다.
c를 알고 있고, 두 변 중 하나의 길이를 알아야 한다면, 다음과 같이 구할 수 있다.
또는
이 방정식으로 직각삼각형의 세 변에 대한 간단한 관계를 알 수 있으므로, 두 변의 길이를 알면 나머지 길이를 알아낼 수 있다. 이 공식을 일반화한 것이 코사인 법칙이며, 이를 이용하면 두 변의 길이와 그 사잇각을 알면 임의의 삼각형의 나머지 변의 길이를 알아낼 수 있다. 두 변이 이루는 각이 직각인 경우 코사인의 법칙은 피타고라스의 원리로 간단히 정리된다.
 에 대하여,
에 대하여,  차원 유클리드 공간
차원 유클리드 공간 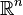 은 집합으로서
은 집합으로서  의
의 




댓글 없음:
댓글 쓰기